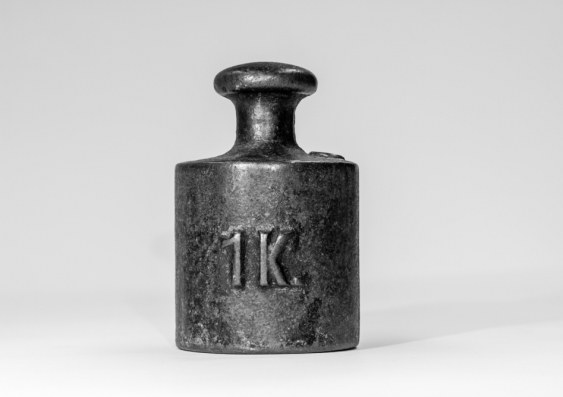We measure stuff all the time – how long, how heavy, how hot, and so on – because we need to for things such as trade, health and knowledge. But making sure our measurements compare apples with apples has been a challenge: how to know if my define kilograms weight or metre length is the same as yours.

Important Announcement – EasyShiksha has now started Online Internship Program “Ab India Sikhega Ghar Se”
Attempts have been made to define the units of measurement over the years. But today – International Metrology Day – sees the complete revision of those standards come into play.
You won’t notice anything – you will not be heavier or lighter than yesterday – because the transition has been made to be seamless define kilograms.
Just the definitions of the seven base units of the SI (Système International d’Unités, or the International System of Units) are now completely different from yesterday.
New definitions of the (SI) standards for the kilogram (kg), metre (m), second (s), ampere (A), kelvin (K), mole (mol) and candela (cd). BIPM, CC BY-ND
How we used to measure
Humans have always been able to count, but as we evolved we quickly moved to measuring lengths, weights and time.
The Egyptian Pharaohs caused pyramids to be built based on the length of the royal forearm, known as the Royal Cubit. This was kept and promulgated by engineer priests who maintained the standard under pain of death.
Metrology in action – weighing the souls of the dead and the Egyptian Royal Cubit (the black rod). Brynn Hibbert
But the cubit wasn’t a fixed unit over time – it was about half a metre, plus or minus a few tens of centimetres by today’s measure.
The first suggestion of a universal set of decimal measures was made by John Wilkins, in 1668, then Secretary of the Royal Society in London.
The impetus for doing something practical came with the French Revolution. It was the French who defined the first standards of length and mass, with two platinum standards representing the metre and the kilogram on June 22, 1799, in the Archives de la République in Paris.
Top Courses in Software Engineering
More Courses With Certification
The new SI definitions
The main problems with the previous definitions were, in the case of the kilogram, they were not stable and, for the unit of electric current, the ampere could not be realised.
And from weighings against official copies, we think the Big K was slowly losing mass.
All the units are now defined in a common way using what the BIPM calls the “explicit constant” formulation.
The idea is that we take a universal constant – for example, the speed of light in a vacuum – and fix its numerical value at our best-measured value, without uncertainty define kilograms.
Reality is fixed, the number is fixed, and so the units are now defined.
We therefore needed to find seven constants and make sure all measurements are consistent, within measurement uncertainty, and then start the countdown to today.
Australia had a hand in fashioning the roundest macroscopic object on the Earth, a silicon sphere used to measure the Avogadro constant, the number of entities in a fixed amount of substance. This now defines the SI unit, mole, used largely in chemistry.
Walter Giardini of the National Measurement Institute Australia holding a silicon sphere as part of the Avogadro project. Brynn Hibbert
From standard to artefact
What of the Big K – the standard kilogram? Today it becomes an object of great historical significance that can be weighed and its mass will have measurement uncertainty.
From today the kilogram is defined using the Planck constant, something that doesn’t change from quantum physics.
The challenge now though is to explain these new definitions to people – especially non-scientists – so they understand. Comparing a kilogram to a metal block is easy.
Technically a kilogram (kg) is now defined:
[…] by taking the fixed numerical value of the Planck constant h to be 6.626 070 15 × 10–34 when expressed in the unit J s, which is equal to kg m2 s–1, where the metre and the second are defined in terms of c and ΔνCs.
Try explaining that to someone!
Authored by David Brynn Hibbert
Empower your team. Lead the industry
Get a subscription to a library of online courses and digital learning tools for your organization with EasyShiksha
Request NowALSO READ: Plastic-free-aravallis-environment-friendly
Get Course: Zero-to-Hero-in-Django-Python-Framework